冬奥会的大雪花里有多少朵小雪花？

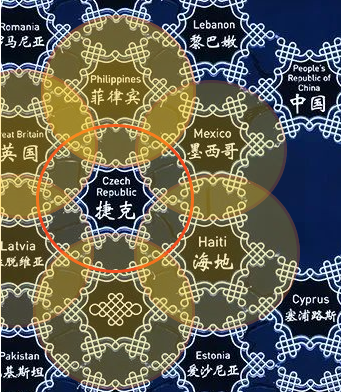
2022年2月4日，北京冬奥会开幕式在国家体育场举行。从引导员入场开始，91 朵代表参赛国家和地区的雪花缓缓飘来，汇聚北京。

在蓝色地球的映衬下，雪花从天而降，遨游天际，“春雪满空来，触处似花开”。一朵朵中国结造型的雪花竞相开放，而后汇聚凝结，形成一朵晶莹如玉的巨大雪花，象征奥林匹克精神的火炬于大雪花中央“点燃”，星火虽微，但在代表参赛国家和地区的小雪花的包围下，更显团结、包容的大国理念。

为什么代表91个参赛国家和地区的小雪花能够正好镶嵌进大雪花，使大雪花呈现如此和谐、完美的形态？其实大雪花中的雪花数量并非91朵，如果你仔细观察，会发现有5朵雪花没有标注国家和地区名字，大雪花中一共有96朵小雪花。

大雪花可以看作一个对称性极好的正六边形，有6条对称轴，所有雪花的数量必然是6的倍数，和91最接近的6的倍数是96。大雪花正是由96朵小雪花镶嵌而成。

大雪花的完美之处不仅于此。在大雪花边界处可以继续拼接小雪花，并且无限延展下去，永无尽头。

另外，每一朵小雪花都内接于一个圆中，这个圆由其他6朵小雪花的尖角拼接而成。每一朵小雪花既是圆的中心，也是其他小雪花的外接圆的组成部分。96朵小雪花你中有我，我中有你，构成了“人类共同的一朵雪花”。

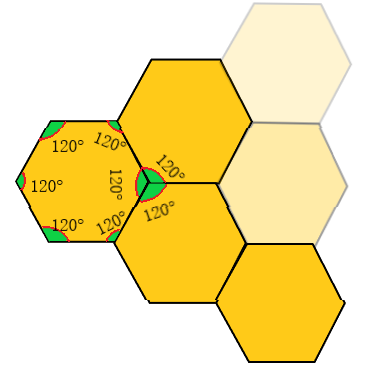
设计师以正六边形作为雪花的基本形态，不仅符合自然规律，也符合数学规律。正六边形具有优雅的数学形态，使得小雪花的拼接可以如此完美、和谐。

正六边形每个内角为120度，3个正六边形拼接时恰好可以形成一个周角（360度），因此正六边形可以不重叠、不留缝隙地拼接，只要数量足够多，可以铺满整个平面，这种现象被称为平面图形的密铺。

除了正六边形还有哪些正多边形可以密铺呢？这样的正多边形需要满足的条件是，其内角度数可以被360整除，因此除正六边形之外，只有正三角形（内角为60度）、正方形（内角为90度）可以密铺。

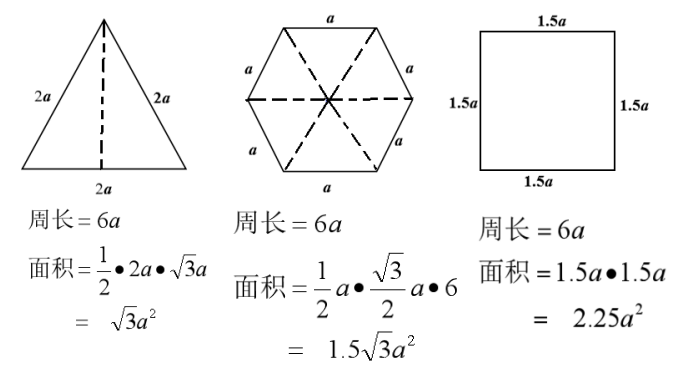
在这3种可以密铺的正多边形中，正六边形又是最特殊的一个。在周长相等时，正六边形的面积最大，这意味着选择正六边形可以让人们用更少的材料围成更大面积。

另外，正六边形的对称轴多达6条，因此它可以经过各式各样的旋转、翻折而不改变形态，具有良好的对称性。

正六边形优雅的数学形态使它在自然界也广受青睐。如蜜蜂建造的蜂巢正是由形如正六边形的巢室组成，似乎建造等边三角形或正方形巢室更简单，但是正六边形结构蜂巢可以让蜜蜂筑巢时用尽可能少的蜜蜡，同时正六边形巢室也更适合养育类圆状的幼虫。此外，正六边形结构蜂巢也比三角形或正方形结构蜂巢更为坚固。

冬奥雪花中的数学之美不止正六边形，场外火炬台上的大雪花被一根“银丝带”环绕，其形状和莫比乌斯环有些类似，晶莹的“雪花”和灵动的“银丝带”之间进行着非匀速的双向同心旋转，尽显轻盈和优雅。

莫比乌斯环是典型的拓扑结构，它的特征是一只小虫可以爬遍整个曲面（两个面）而不用跨越它的边缘，这个过程可以无限进行。

正如火炬台动态雕塑设计团队成员清华大学美术学院副教授陈洛奇所述，“‘银丝带’类似莫比乌斯环的造型设计中蕴含了‘奥运精神的源远流长、永恒无限，无论从哪里开始我们终能相遇，彰显人类命运共同体’的哲学理念。”

世界上的美是相通的。数学为视觉美提供了无限的可能性，数学的理性不仅不会制约原本感性的艺术，反而会为艺术的直觉和想象力创造更多空间。

这一点在江苏凤凰科学技术出版社的初中数学教材和数学学习用书中有很多体现。

苏科版数学教材让孩子从数学学习中发现艺术、发现美，继而让孩子自觉去探索美中蕴含的数学本质。

打开课本，寻找更多数学之美吧！