二元一次方程组的解法

【提炼】

随着学习的深入，我们发现用二元一次方程组可以来刻画现实世界两个量之间的两组数量关系，这一新的数学模型可以将一些实际问题转化为方程组来解决，而二元一次方程组的求解也是通过代入消元和加减消元的方法，把二元转化为一元.显然，转化的思想贯穿于本章的始终.

熟练掌握二元一次方程组的解法是解决实际问题的前提，在求解过程中，必须分析其特点，灵活、便捷地选用消元方法，真正做到化繁为简、化难为易.

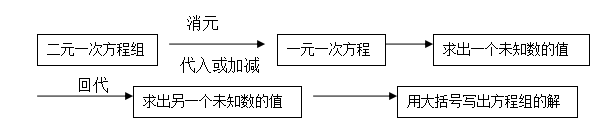
解方程组的步骤可用框图表示成：

例1 袋子里有若干大小相同的两种小球，分别标有数字2和3．

⑴小明从中摸出10个球．请你设计一张表格，列出小明摸出球的所有可能情况及两球的数字和；若摸出的两球数字之和是23，则摸出的两种球各是多少？

⑵小明从中摸出的两种球数目相等，且数字之和是35，则一共摸出了多少球？

⑶小明从中摸出的两种球的数字之和是38，则小明最多可摸出多少个数字是3的球？

分析：第⑴、⑵两小题可分别从球的数目及数字和两个角度来构造方程组；第⑶小题未知摸出球的数量关系，根据数字和可得关于两球数目的二元一次方程，对于一般意义的二元一次方程组的解是不确定的，注意到球的数目是自然数，由题意，要使摸出的一种球数最多，则另一种球数必然最少．

 解  ⑴　填表请读者完成．第二问的解答有两种方法：一是通过表中发现结论；二是建立方程组求解．

设摸出标有数字2，3的球分别为x，y个，于是有

即摸出7个标有数字2的球，3个标有数字3 的球.

⑶　由题意，得  2x+3y=38．①　　由于x、y都是自然数，因此在①式中，当x=0时，y取得最大值，显然x=0时y不是整数，所以x=1,则y=12．

即小明最多摸出12个标有数字3的球．

评注：可以看出，解题中用到了列举法、构造一元一次方程、二元一次方程组及二元一次方程的整数解等知识．对于一个实际问题，我们可以从不同的角度去思考．学会多解，不仅可加深对题目数量关系的理解，找到简捷的分析方法和解题途径，还可以促使我们多方面、多角度地思考问题，提高综合运用数学知识的能力．

例2  已知某电脑公司有Ａ型、B型、C型三种型号的电脑，其价格分别为A型每台6000元，B型每台4000元，C型每台2500元．某学校计划将100500元钱全部用于从该公司购进其中两种不同型号的电脑36台，共有几种不同的购买方案？若不准备同时购买价格较高的两种型号的电脑，请你列出关于购进的两种型号电脑台数的二元一次方程组．

分析：显然共有三种不同的购买方案．根据题意只能同时购买A型、C型或B型、C型的电脑．所求方程组不唯一，分别从电脑的台数及购买的钱数寻找等量关系．

评注：这是一道多结论、开放性的实际问题，只有经过认真审题，仔细分析，才能作出正确解答．