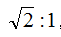我敢打赌，你可能有哪一天不吃饭，但不可能有哪一天不接触A4纸，A4纸，这个生活中最简单、最司空见惯的东西，你有想过它背后的问题吗？

比如它为什么叫A4纸？不叫X1纸？（这样岂不是更霸气！）

为什么尺寸是210mm*297mm，为什么不是200*300？（这是要逼死强迫症吗？）

为什么它不设计成正方形的？（连叠个纸飞机都要裁一刀！）

为什么它不设计得大一点？（外卖的时候连垫桌子都不够！）

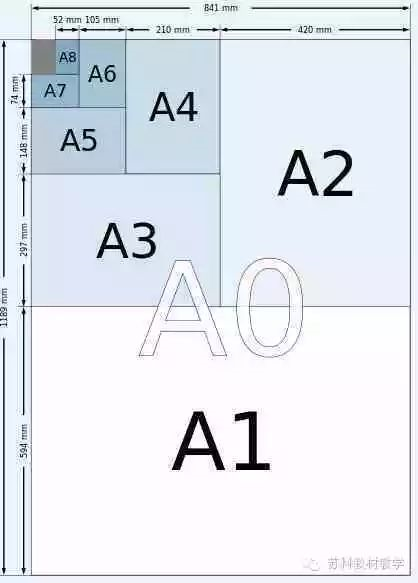
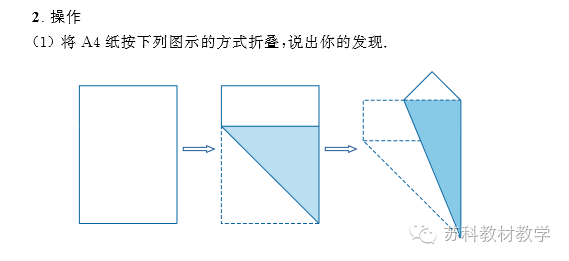
哪里有工业设计，哪里就有严谨的德国人，即使是小小的一张纸也不例外，早在19世纪20年代，德国工业标准体例就将日常用纸纳入其下。

几经演变， ISO 216定义了今日世界上大多数国家所使用纸张尺寸的国际标准，命名为A、B、C三类（说叫X纸的，是X战警看多了吗），如A0、A1、B0、B1、C2······，其中C号纸主要使用于信封尺寸，每种纸名后面携带的编号可以理解为相互对折的次数，如A4纸实际上就是A0纸第四次对折的纸张大小。

聪明如你，你一定发现A号纸的长宽比例似乎蕴含某种规律，它们好像“长得差不多”，而且看上去视乎很“和谐”，很具有规律的“美感”，难道这个比例是传说中“黄金比”，即承载古典主义美学精髓的1.618：1？然而用计算器算一算，很快就发现A4纸长与宽的比是1.4142···：1，而不是1.618：1，1.4142···是什么？！

翻开苏科版初中《数学实验手册》八年级上册，“打印纸中的数学”助你解开疑惑！

别说话，随手拿一张A4纸跟我做：

别告诉我你什么也没发现！折叠后可以看到第二张图下方正方形的对角线和A4纸的长是重合的，如果设A4纸的宽是1，显然第二张图下方正方形的对角线的长是根号2

而这条对角线和A4纸的长是重合的，因此A4纸的长与宽的比是

也就是上面计算器算出的1.414：1。可是，为什么要这么设计呢？

别说话，继续跟我做：

1.414：1是最适合于标准化纸张型号的比例，以A0到A6这个区间来说，A0=841mmx1189mm ，面积正好是1平方米，不断将长边对折分割并且不会改变原来的比例关系，而且在工厂的剪裁中可以做到最大程度的避免浪费，甚至是完全没有浪费，这个看似无厘头的比例却是工业实用性与几何美学最完美的结合！