从古至今，数学的美让人为之崇拜，甚至痴迷，而在人类的历史上曾经有一个数字引起了一场追杀，并导致了人类的认知危机。

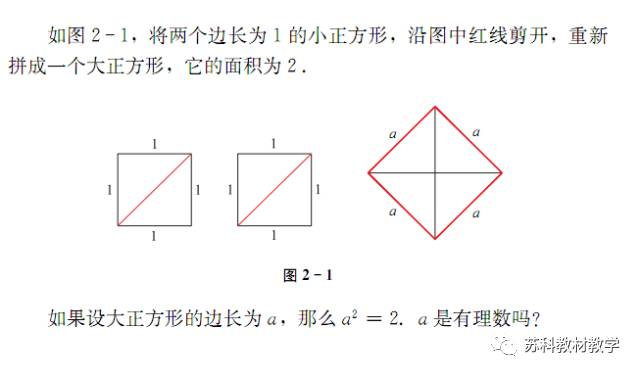
      这一切要从西方发现“毕达哥拉斯定理（勾股定理）”的古希腊哲学家毕达哥拉斯说起。“毕达哥拉斯学派”对数十分崇拜，甚至带有浓浓的宗教色彩，他们认为宇宙是依据数字而构建。数已经上升到高得不能再高的地位——万物皆数。而他们所说的“数”是整数,或者整数之比（分数）,也就是说宇宙万物归根到底都是整数比例的问题。

     但是毕达哥拉斯的徒弟希帕索斯却发现，边长为1的等腰直角三角形的斜边的长度似乎是一个神秘的、无限的数，它无法表示为整数的比例！这个数动摇了整个学派的根基，它变成了最高机密和最大忌讳。

          这个数是人类发现的第一个无理数，它的出现不仅是对毕达哥拉斯学派的致命打击，也严重伤害了当时全体希腊人的信仰。对于古希腊人来说，这样的数是多么毁灭人信仰、破坏人安全感，是多么可怕的数字，更糟糕的是，面对这一荒谬人们竟然毫无办法。这就在当时直接导致了人们认识上的危机，从而导致了西方数学史上一场大的风波，史称“第一次数学危机”。

       毕达哥拉斯学派对希帕索斯下了追杀令，他被学派教徒抓获，直接扔进大海。从现有的资料来看，因无理数而死的人还不止希帕索斯一个，因为古希腊数学家普罗科拉斯在给《几何原本》作注时写道：“据说，首先泄露无理数秘密的人们都丧了命，因为对所有不能表达的和不定形的东西，都要严守秘密，凡是揭露和过问的人，必会遭到毁灭，并万世都被永恒的波涛吞噬。”

     一个小小的无理数引起了一场人类的认知危机与追杀，直到1872年，德国数学家戴德金用“有理数的分割”来定义无理数，并建立了实数理论，希帕索斯引发的第一次数学危机，持续了2000多年后，至此才算圆满化解。

      那么，我们究竟怎么证明当年杀死希帕索斯的“边长为1的等腰直角三角形的斜边的长度  ”不可以表示为毕达哥拉斯的“圣数”——整数之比（分数）呢？

      苏科版初中《数学》教材七年级上册“第2章 有理数”中就有答案：

        通过以上的讨论，我们发现，大正方形的边长无法表示成两个整数之比。那么这样一个数究竟是什么样的？是真实存在的吗？在数轴上，它在哪个位置？下面的数学实验告诉我们，无理数的的确确存在，它就在数轴上。